“Read Euler: he is our master in everything”. (Pierre-Simon Laplace)
Leonhard Euler (pronounced ‘Oiler’) was a Swiss mathematician (as well as being a physicist, astronomer, geographer, logician, and an engineer) who lived and worked in the 18th Century. He was one of the greatest mathematicians of all time.
This paper starts where the paper “Support Metrics Part 1” finished, with the question “What is Euler’s Number ‘e’, and where does it come from?
Simplistically, Euler’s number is a constant which equals – approximately – 2.7182818284590452353602874713527… (but it is not referred to as Euler’s Constant, that is a different value, represented by the Greek letter gamma – ɣ). It is an ‘irrational number’, like Pi, it cannot be represented as a fraction because there are an infinite number of digits after the decimal point.
In the field of Support Engineering it is used to determine the probability of survival, for time ‘t’, of an engineered component using the function R(t) = e-λt. However it can be used to describe Exponential Growth as well as Exponential Decay.
This paper aims to explain why this particular number is used and how it is determined, and to do so in layman’s terms.
Growth and decay
In the first paper, “Support Analysis – Understanding the Numbers – Support Metrics Part 1,” we saw that the exponential distribution can have both positive (Growth) and negative (Decay) versions. We also saw that we can use ‘e’, in combination with the appropriate failure rate (λ), to predict the probability of survival of a component for a given time ‘t’ using the function R(t) = e-λt.
Exponential Growth = eλt

Exponential Decay = 1/eλt . More commonly written e-λt .
The next question we have to answer is why this particular number? Where does it come from?
Deriving 'e'
Understanding where this constant, 2.7182818284590452353602874713527… comes from is most easily achieved if we start by considering how interest works on a sum of money that we have invested, i.e. if we examine how “Compound Interest”, a specific case of Exponential Growth, works. Imagine that we have invested a sum of £1 – at a ‘nominal’ interest rate of 100% per annum.
In this simple example, we would expect to get a return at the end of 1 year of £2.
Output = 1 x (1 + i)
£1 + (1 x i) = £1 x (1 + 1) = £2 (i = interest rate = 100% – i.e. 1 – in this example).
But now suppose that we withdrew our money after 6 months… then we would still expect to receive some interest, i.e. we would expect to receive half of the interest:
Output = £1 x (1+ i/2) = £1 x (1+0.5) = £1.50
But that £1.50 could then be reinvested for a further 6 months…
Output = £1.50 x (1+i/2) = £1 x (1+0.5) = £2.25.
Hence ‘Compounding’ the interest at 6 monthly intervals yields significantly better returns than compounding at the end of 12 months.
NOTE: The total interest earned in the year = £1 x (1 + i/2)(1 + i/2) which can be written (1 + i/2)2. Note that the power ‘2’ corresponds to the number of periods over which the interest is compounded, i.e. two 6 month periods in this example.
So what if we compound the interest every 3 months?
1st Period Output = £1 x (1+ i/4) = £1 x (1+0.25) = £1.25
2nd Period Output = £1.25 x (1+ i/4) = £1.25 x (1+0.25) = £1.5625
3rd Period Output = £1.5625 x (1+ i/4) = £1 x (1+0.25) = £1.953125
4th Period Output = £1.953125 x (1+ i/4) = £1 x (1+0.25) = £2.44140625
Compounding the interest at 4 intervals yields an even greater return, but note that the improvement is not as great as that that was achieved when increasing the periods from 1 to 2.
NOTE: The interest earned = £1 x (1 + i/4)(1 + i/4)(1 + i/4)(1 + i/4) which can be written (1 + i/4)4
This can be written as a general rule i.e. The interest earned = £1 x (1 + i/n)n Where ‘n’ is the number of periods at which we compound the interest.
Using this general rule, then:
Compounding the interest at monthly Intervals yields: £1 x (1+i/12)12 = (1.083334)12 = £2.6130548…
Compounding the interest at weekly intervals yields: £1 x (1+i/52)52 = (1.01923077)52 = £2.69259695…
Compounding the interest at daily intervals yields: £1 x (1+i/365)365 = (1.01923077)365 = £2.7145674820…
NOTE: That the interest rate that results from this compounding of the ‘Nominal Rate’ is referred to as the “Annual Equivalent Rate” [AER].
What would happen then if we if we compounded the interest every minute, or every second?
The result would start to approach 2.7182818284590452353602874713527…

If the number of periods is infinite – then the figure, for a rate of 100% i.e. 1 – is Euler’s Number ‘e’
This is expressed as
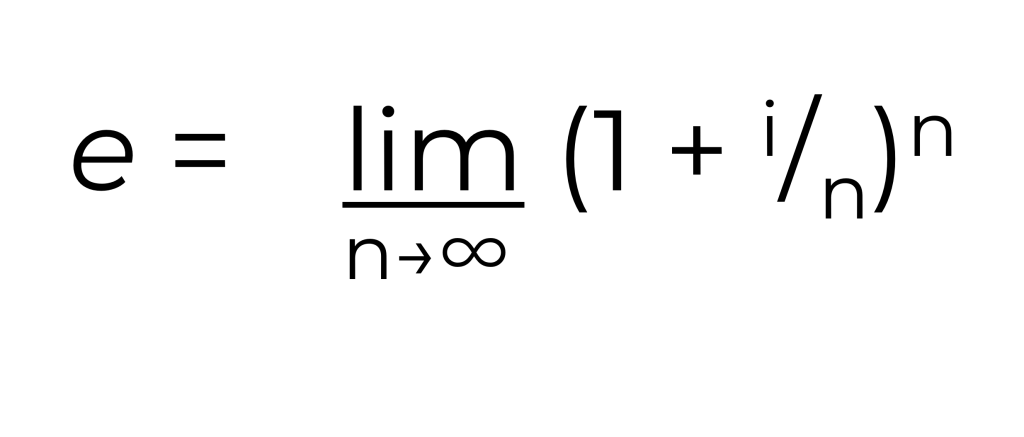
Where:
i is the interest rate
n is the number of periods over which that interest is compounded
We can substitute Euler’s Number in the calculations above – e.g. the return on an investment of £1 at a nominal interest rate of 100%, for a period of 1 year = £1 * 2.71828 = £2.72
We can now modify this equation to take account of different interest rates and different periods of time. To illustrate; consider the expected return on a sum of £50 invested at 25% for 5 years.
The return would be £50 x 2.718280.25 x 5 = £174.52
This would be written as £50 x e0.25×5 = £174.52
We do not need to memorise the value of ‘e’ however as it is provided as a function on our calculators and as a function within Excel.
If the exponent applied to e is positive, we see exponential growth:

If the exponent applied to e is negative, we see exponential decay:

Which is where we started…
In addition to calculating interest and in predicting the probability of survival when conducting Reliability and Supportability Engineering, Euler’s number ‘e’ is used in many other fields.
For example, it is used to predict the growth of bacteria, to predict radioactive decay rates (when using Carbon(14) to date organic material for example) and in electronics to predict the discharge rates of capacitors.

About the Author
Peter has been involved in Defence support for all of his working life, initially in the Army and then as a specialist in Supportability Engineering.
He has extensive experience as a lecturer and trainer in Supportability Engineering; he has been actively engaged in the development and training of US and UK Defence Standards, including ASD S-Series specifications.
As an Army veteran, Peter served in the UK, Canada (BATUS), and Germany maintaining Army and Commando aircraft, he has operated on land and at sea, having deployed on Royal Navy [RN] and Royal Fleet Auxiliary [RFA] vessels.
Connect with Peter on LinkedIn

About Aspire
What does Aspire do? Almost every organisation on the planet uses equipment to deliver its service. Very few are always
happy with the performance of that equipment. We train, guide and
collaborate with organisations to design support solutions that keep
equipment performing, so they can deliver their service, consistently and
effectively.
Follow Aspire on LinkedIn
